二分木の直径を求める問題を幅優先探索で解いてみる

今回は「二分木の直径を幅優先探索で求める」アルゴリズムについて説明します。
※実際にpaiza.IOなどの実行環境に貼り付けて、適宜printを入れて処理を追っていただけると内容が理解しやすくなると思います。
https://paiza.io/ja

前提条件

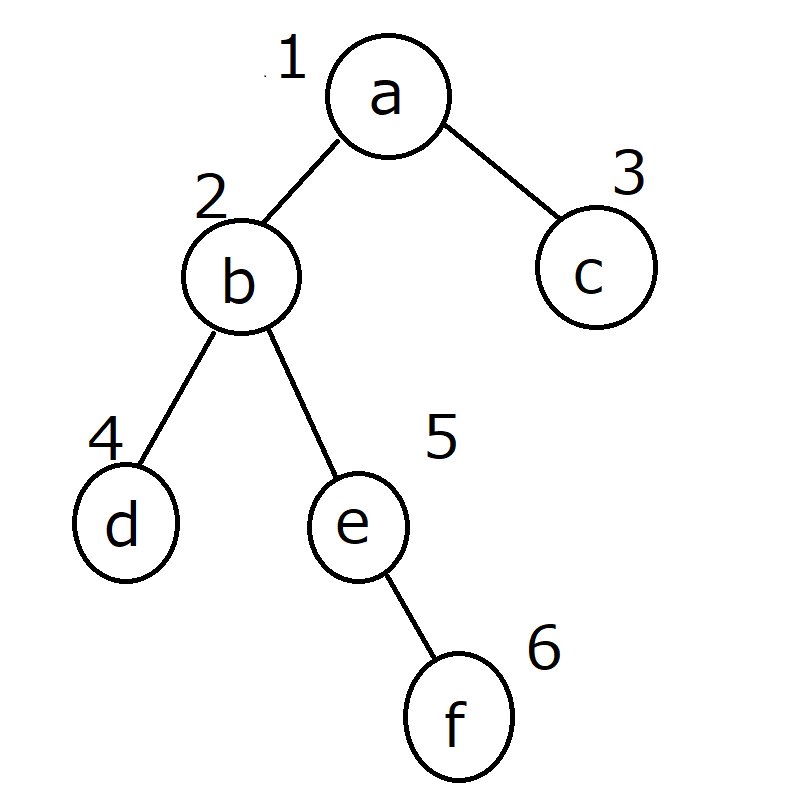
二分木は画像のようなグラフ構造をしています。
丸い点をノード、ノードを結ぶ線をエッジと呼びます。
エッジの距離は全て1とします。
言語はPythonを使用します。

二分木の直径について

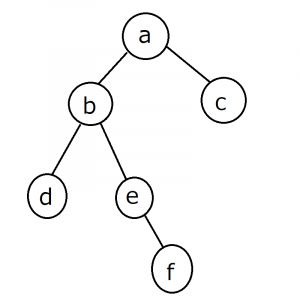
二分木の直径は、互いに最も遠いノード同士の距離から求めることができます。
以下の手順で求めることができます。

任意のノードから一番遠いノードを幅優先探索(後述)で求める
- 例えばaから一番遠いノードを幅優先探索で求めるとfになります。
1で求めたノードから一番遠いノードを幅優先探索で求める
- fから一番遠いノードを幅優先探索で求めるとcになります。
1と2で求めたノード同士の距離が直径になる
- cとfの距離4が直径になります。
  ※深さ優先探索でも求めることができます。(後述)

上記を踏まえ、以下の順番で実装を進めてみます。

幅優先探索であるノードから全てのノードへの距離を返す関数
幅優先探索であるノードから一番遠いノードへの距離を返す関数
2で作った関数の引数を修正し、一番遠いノード同士の距離を取得する

幅優先探索とは？

幅優先探索は、ノードの隣接するノードを全て探索、さらに隣接するノードを全て探索・・・と繰り返していき、隣接するノードがなくなるまで探索を繰り返していくアルゴリズムです。
深さ優先探索との違いは後述します。

1.幅優先探索であるノードから全てのノードへの距離を返す関数を作る

from collections import deque
import numpy

# データの関係をMapで保持する
binaryTree = {
    'a': ['b', 'c'],
    'b': ['a', 'd', 'e'],
    'c': ['a'],
    'd': ['b'],
    'e': ['b','f'],
    'f': ['e']
}

def calcAllNodesAndDists(start) :
    # 作業用キュー
    queue = []
    # すでに訪問したノードの距離
    distances = {}

    # 起点を格納する
    distances[start] = 0
    queue.append(start)

    while len(queue) != 0 :
        node = queue.pop(0)

        # binaryTreeにない場合スキップ
        if not binaryTree.get(node):
            continue

        # 距離が格納されていない、つまり未訪問の場合のみ距離を更新し、隣接するノードをqueueに追加する
        for nextNode in binaryTree[node]:

            if distances.get(nextNode) is None :
                distances[nextNode] = distances.get(node) + 1
                queue.append(nextNode)

                # 出力テスト用
                print (queue, distances)

    return distances

print(calcAllNodesAndDists('a'))

処理を解説していきます。

1-1.データの関係をMapで保持する

初めに、辞書配列で二分木の構造を定義します。
keyにはノードの名前、valueには隣接するノードを定義します。

binaryTree = {
    'a': ['b', 'c'],
    'b': ['a', 'd', 'e'],
    'c': ['a'],
    'd': ['b'],
    'e': ['b','f'],
    'f': ['e']
}

1-2.calcAllNodesAndDistsについて

あるノードから全てのノードへの距離を返す関数です。
幅優先探索を使って求めています。

この処理を今回のアルゴリズムに置き換えて説明していきます。
※引数はaを入れた場合として説明しています。

1-2-1.queueに起点のノードを入れ、distancesに起点のノードからの距離(つまり0)を入れる

この時の値
queue=[a] distances={'a': 0}

1-2-2.while len(queue) != 0 ループ内の処理

queueから先頭の要素を取り出します。
node='a'になります。
node = queue.pop(0)

もしも、binaryTreeに存在しないノードが入っている場合は、スキップします。
'x'など存在しないノードを引数に入れた場合の処理になります。

        if not binaryTree.get(node):
            continue

1-2-3.ノードと隣接するノードの距離を計算して、queueとdistancesに追加する

for nextNode in binaryTree[node]:の中では、隣接するノードをqueueに、隣接するノードへの距離を計算してdistanceに追加します。
aの場合、隣接するノードはb,cなので、それぞれ計算していきます。

まずbまでの距離を計算します
bはaの一つ隣なので、以下の処理で距離を1加算します。
distances[nextNode] = distances.get(node) + 1
次にqueueにbを追加します。
この時点で以下になります。
queue=['b'] distances={'a': 0, 'b': 1}

次にcまでの距離を調べます。
cもaの一つ隣なので、同じように距離を1加算し、queueに追加します。
この時点で以下になります。
queue=['b', 'c'] distances={'a': 0, 'b': 1, 'c': 1}

1-2-4.以下whileループ内を繰り返します

queueに入ったノードについても同じように、隣接するノードまでの距離を計算していきます。
bに隣接するノードはa,d,eがあります。
このとき、aもqueueに入れてしまうと、
aに隣接するノードを探索→bに隣接するノードを探索→aに隣接するノードを探索→bに隣接するノードを探索・・・
と探索が無限に繰り返されてしまい、タイムアウトしてしまいます。

これを防ぐために、「すでに訪問したノード(=distancesに存在するノード)は距離の計算の対象外とする」処理を入れています。

それがこのif文になります。
if distances.get(nextNode) is None :

bに隣接するノードのうち、d,eまでの距離を調べ、queueとdistanceを更新します。
cには隣接するノードがないので、queueとdistanceの更新は行いません。
queue=['c', 'd'] distances={'a': 0, 'b': 1, 'c': 1, 'd': 2}
queue=['c', 'd', 'e'] distances={'a': 0, 'b': 1, 'c': 1, 'd': 2, 'e': 2}

同様に処理を繰り返します。
dには隣接するノードがなく、eにはfが隣接するノードとして存在するので、queueにfが入りdistanceが計算されます。
queue=['f'] distances={'a': 0, 'b': 1, 'c': 1, 'd': 2, 'e': 2, 'f': 3}
queue=[] distances={'a': 0, 'b': 1, 'c': 1, 'd': 2, 'e': 2, 'f': 3}

このような流れで各ノードへの距離が算出されるのがわかります。

2.幅優先探索であるノードから一番遠いノードへの距離を返す関数

次にこのコードを少しアレンジします。
ある点から、一番遠いノードと距離を返すようにしています。

from collections import deque
import numpy

# データの関係をMapで保持する
binaryTree = {
    'a': ['b', 'c'],
    'b': ['a', 'd', 'e'],
    'c': ['a'],
    'd': ['b'],
    'e': ['b','f'],
    'f': ['e']
}

def calcFarestNodeAndDist(start) :
    # 作業用キュー
    queue = []
    # すでに訪問したノードの距離
    distances = {}

    # 起点を格納する
    distances[start] = 0
    queue.append(start)

    max = 0
    farestNode = "not found"

    while len(queue) != 0 :
        node = queue.pop(0)

        # binaryTreeにない場合スキップ              
        if not binaryTree.get(node):
            continue

        # 距離が格納されていない、つまり未訪問の場合のみ距離を更新し、隣接するノードをqueueに追加する
        for nextNode in binaryTree[node]:
            if distances.get(nextNode) is None :
                distances[nextNode] = distances.get(node) + 1
                queue.append(nextNode)

                if distances[nextNode] > max :
                    max = distances[nextNode]
                    farestNode = nextNode

    return max, farestNode

print(calcFarestNodeAndDist('a'))

距離がmaxを超えるたびに更新していき、最終的に一番遠いノードの距離と名前を返すという関数になっています。
実際に実行すると、
(3, 'f')
が返ってきます。

3.2で作った関数の引数を修正し、一番遠いノード同士の距離を取得する

さらに、コードをアレンジします。

from collections import deque
import numpy

# データの関係をMapで保持する
binaryTree = {
    'a': ['b', 'c'],
    'b': ['a', 'd', 'e'],
    'c': ['a'],
    'd': ['b'],
    'e': ['b','f'],
    'f': ['e']
}

def calcFarestNodeAndDist(start) :
    # 作業用キュー
    queue = []
    # すでに訪問したノードの距離
    distances = {}

    # 起点を格納する
    distances[start] = 0
    queue.append(start)

    max = 0
    farestNode = "not found"

    while len(queue) != 0 :
        node = queue.pop(0)

        # binaryTreeにない場合スキップ              
        if not binaryTree.get(node):
            continue

        # 距離が格納されていない、つまり未訪問の場合のみ距離を更新し、隣接するノードをqueueに追加する
        for nextNode in binaryTree[node]:
            if distances.get(nextNode) is None :
                distances[nextNode] = distances.get(node) + 1
                queue.append(nextNode)

                if distances[nextNode] > max :
                    max = distances[nextNode]
                    farestNode = nextNode

    print (farestNode)

    return max, farestNode

print(calcFarestNodeAndDist(calcFarestNodeAndDist('e')[1]))

あるノードから一番遠いノードを求める→そのノードから一番遠いノードを求める
と一番遠いノード同士の距離、つまり直径が求まるということです。

eを代入すると
→一番遠いノードc
→cから一番遠いノードf
このとき距離は4
なので、直径は4になる、ということですね。

4.深さ優先探索で求めたい場合

深さ優先探索で求めたい場合は、
node = queue.pop(0)
でqueueの先頭から取得していた箇所を
node = queue.pop()
でqueueの末尾から取得するように変更するだけです。

探索時に、隣接するノードはqueueの末尾に追加されます。
pop(0)で先頭からとると、次に探索されるのは並列して隣接するノードになるので、幅優先探索になります。
pop()で末尾からとると、次に探索されるのは隣接するノードのさらに隣接するノードなので、深さ優先探索になります。

実際にprintを入れてみて探索の順序を確認してみましょう。

4-1.幅優先探索

queue=['b'] distances={'a': 0, 'b': 1}
queue=['b', 'c'] distances={'a': 0, 'b': 1, 'c': 1}
queue=['c', 'd'] distances={'a': 0, 'b': 1, 'c': 1, 'd': 2}
queue=['c', 'd', 'e'] distances={'a': 0, 'b': 1, 'c': 1, 'd': 2, 'e': 2}
queue=['f'] distances={'a': 0, 'b': 1, 'c': 1, 'd': 2, 'e': 2, 'f': 3}
([], {'a': 0, 'b': 1, 'c': 1, 'd': 2, 'e': 2, 'f': 3})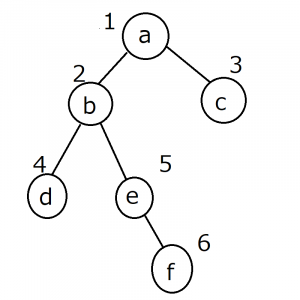

隣接するノードを全て調べる→さらに隣接するノードを全て調べる、という方法で探索しています。

4-2.深さ優先探索

queue=['b'] distances={'a': 0, 'b': 1}
queue=['b', 'c'] distances={'a': 0, 'b': 1, 'c': 1}
queue=['d'] distances={'a': 0, 'b': 1, 'c': 1, 'd': 2}
queue=['d', 'e'] distances={'a': 0, 'b': 1, 'c': 1, 'd': 2, 'e': 2}
queue=['d', 'f'] distances={'a': 0, 'b': 1, 'c': 1, 'd': 2, 'e': 2, 'f': 3}
([], {'a': 0, 'b': 1, 'c': 1, 'd': 2, 'e': 2, 'f': 3})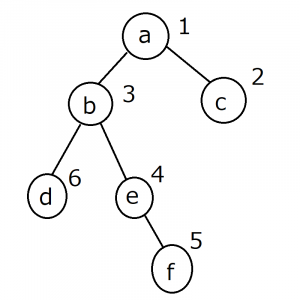

隣接するノードを調べる→さらにそのノードに隣接するノードを調べる→隣接するノードがなくなるまで続け、なくなったら一つ前に戻って同様に探索する、という方法で探索しています。

参考文献および類似問題

https://leetcode.com/problems/diameter-of-binary-tree/

プロフィール

T Kato: 新卒でSIerに入社し、その後メンバーズに転職。
フロント案件を主に経験していたが、インフラ周りのスキルを身につけたいという思いから社内公募制度を利用し、2022年12月に異動。

DevOps ナレッジ広場

AtCoderの言語アップデート(2023)にD言語環境で参加しました

SQL速度向上のために過去に自分が意識していた書き方の効果を実際に検証してみた

jsonファイルをjqで絞り込んでS3に送信するGithub Actionsワークフローを作ってみた

VSCodeにlinterとformatterを入れて生産性・品質向上

二分木の直径を求める問題を幅優先探索で解いてみる

velo by wixとgithubを連携してみた

JMeterで負荷テストのシナリオ作成とGCEを使ったリモート実行

条件によってはお得かも AWS Synthetics Canary

TerraformでGAになったGoogle Cloud Platform（GCP）のCloud Run Jobs（ジョブ）を構築する

二分木の直径を求める問題を幅優先探索で解いてみる

前提条件

二分木の直径について

幅優先探索とは？

1.幅優先探索であるノードから全てのノードへの距離を返す関数を作る

1-1.データの関係をMapで保持する

1-2.calcAllNodesAndDistsについて

1-2-1.queueに起点のノードを入れ、distancesに起点のノードからの距離(つまり0)を入れる

1-2-2.while len(queue) != 0 ループ内の処理

1-2-3.ノードと隣接するノードの距離を計算して、queueとdistancesに追加する

1-2-4.以下whileループ内を繰り返します

2.幅優先探索であるノードから一番遠いノードへの距離を返す関数

3.2で作った関数の引数を修正し、一番遠いノード同士の距離を取得する

4.深さ優先探索で求めたい場合

4-1.幅優先探索

4-2.深さ優先探索

参考文献および類似問題

プロフィール

最新の投稿